Coordinate Converter

Formula For Polar to Cartesian Conversion

x = r * cos(θ): This gives the x-coordinate in Cartesian coordinates.
y = r * sin(θ): This gives the y-coordinate in Cartesian coordinates.

Example Conversion of Polar to Cartesian

Polar coordinate Radial Distance ( r ) : 5
Polar coordinate Angle ( θ ) : 20° degrees
x = 5 * cos(20)
y = 5 * sin(20)

Where, 
cos(20°) = 0.9396926
sin(20°) = 0.34202014332

So, 
x = 5 * 0.9396926 = 4.70
y = 5 * 0.34202014332 = 1.71

Formula for Cartesian to Polar Conversion

r = √(x^2 +y^2): This gives the radial distance in Polar coordinates.
θ = arctan(y/x): This gives the angle in Polar coordinates.

Example Conversion of Cartesian to Polar

Lets take,
x = 4.70 
y= 1.71

r = √(x^2 +y^2)
r = √( 4.70^2 + 1.71^2) = √( 22.09 + 2.92 )
r = √(25.01) 
r = 5.00

θ = arctan(y/x)
θ = arctan(1.71/4.70)
θ = arctan(0.363)
θ = 19.95

Polar Coordinates

Polar Coordinate is nothing but a point in a plane. It just specifies that a point is in a fixed distance and at a particular angle from the source. For example an analog clock 12 will be 90 degrees and the distance from center to the number is 10 cm. This is an analogy of polar coordinate system

Components of Polar Coordinates

The Radial Distance (r): The radial distance is the length of the line from the Pole to the point. 

The Angle (θ): The angle is measured in both degrees and radians from the reference direction to the line connecting the pole and the point.   

Visual Representation of Polar Coordinates

Visual aids, such as graphs and diagrams, can help illustrate how Polar coordinates work and are used in practice.

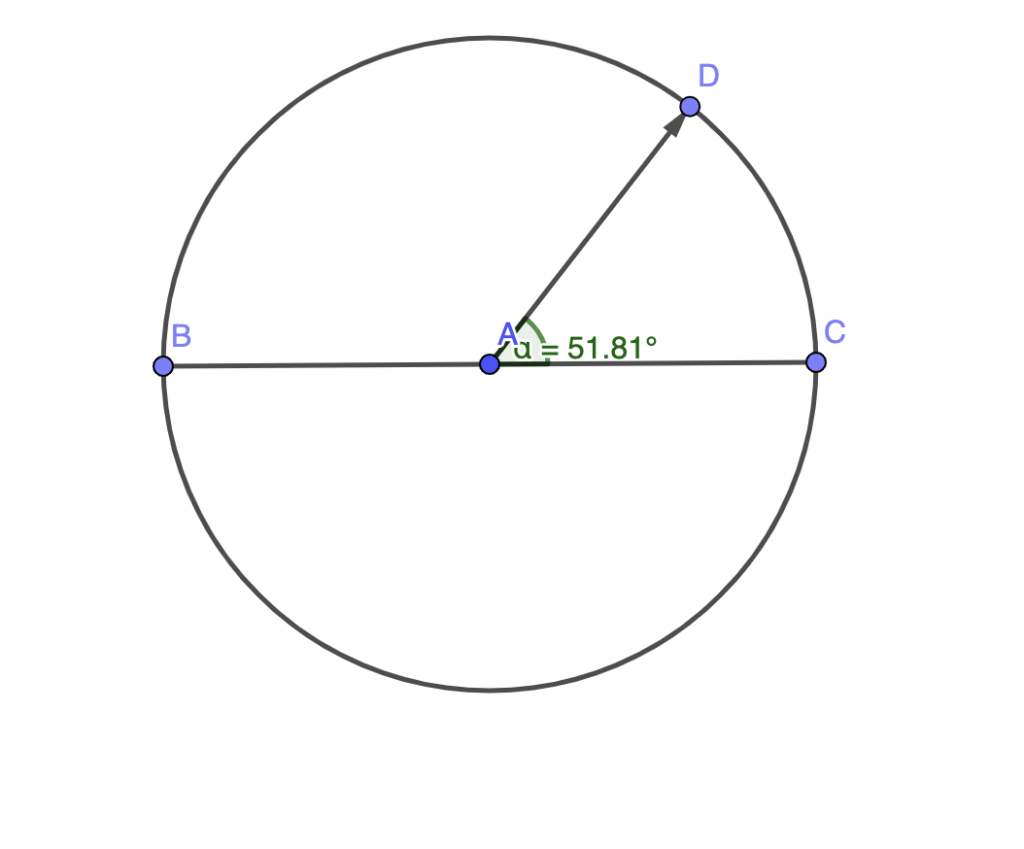
 Real-World Applications of Polar Coordinates

There are many real life applications for polar coordinates like astronomy (celestial coordinates), engineering (mechanical systems with rotational symmetry), and physics (circular motion).

One of the main applications is that the lidar sensors spin and get distance thus, they are represented as polar coordinates when viewed as raw data. 

To view this Lidar Data in a map, the polar coordinate is converted into cartesian and plotted in a map. 

Cartesian Coordinates

Cartesian Coordinate is also called as the rectangular coordinare, which is used to locate a point in a plane by specifying its distance from 2 perpendicular lines, usually the x-axis and the y-axis. 

Cartesian coordinates, also known as rectangular coordinates, locate a point in a plane by specifying its distances from two perpendicular lines, usually called the x-axis and y-axis. Where, 

x-coordinate: The distance from the point to the y-axis, measured parallel to the x-axis.

y-coordinate: The distance from the point to the x-axis, measured parallel to the y-axis.

Visual Representation of Cartesian Coordinates

Visualize how Cartesian coordinates form a grid system and how points are located on it.

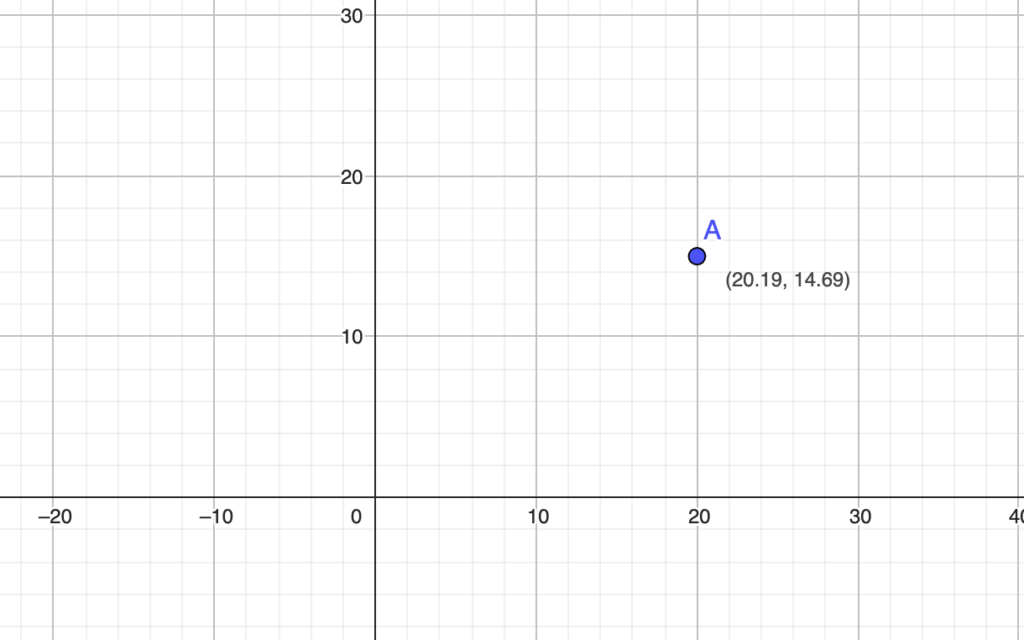
Real-World Applications of Cartesian Coordinates

• Precise location in GPS and navigation systems.
• Fundamental tool for physics and engineering calculations.
• Used in computer graphics for image manipulation.
• Used for data analysis and visualization in statistics.
• In architectural design and structural planning.